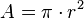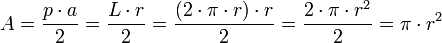jueves, 3 de junio de 2010
CONCLUSIONES
Toda función cuadrática f(x) = ax2 + bx + c, representa una parábola tal que:
Su forma depende exclusivamente del coeficiente a de x2.
Los coeficientes b y c trasladan la parábola a izquierda, derecha, arriba o abajo.
Si a > 0, las ramas van hacia arriba y si a < 0, hacia abajo.
Cuanto más grande sea el valor absoluto de a, más cerrada es la parábola.
Existe un único punto de corte con el eje Y, que es el (0, y) o (0, c).
Los cortes con el eje X se obtienen resolviendo la ecuación ax2 + bx + c=0, pudiendo ocurrir que lo corte en dos puntos, en uno o en ninguno.
La primera coordenada del vértice es Xv = -b/2a.
miércoles, 2 de junio de 2010
Circunferencia
Una circunferencia es un conjunto de puntos del plano equidistantes de otro fijo, llamado centro; esta distancia se denomina radio. Sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.
Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono de infinitos lados, cuya apotema coincide con su radio.
La circunferencia de centro en el origen de coordenadas y radio 1 se denomina circunferencia unidadElementos de la circunferencia
Existen varios puntos, rectas y segmentos, singulares en la circunferencia:
- centro, el punto interior equidistante de todos los puntos de la circunferencia;
- radio, el segmento que une el centro con un punto de la circunferencia;
- diámetro,o cuerda mayor, el mayor segmento que une dos puntos de la circunferencia, y lógicamente, pasa por el centro;
- cuerda, el segmento que une dos puntos de la circunferencia; las cuerdas de longitud máxima son los diámetros;
- recta secante, la que corta a la circunferencia en dos puntos;
- recta tangente, la que toca a la circunferencia en un sólo punto;
- punto de tangencia, el de contacto de la tangente con la circunferencia;
- arco, segmento curvilíneo de puntos pertenecientes a la circunferencia;
- semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.
Longitud de la circunferencia
La longitud  de una circunferencia es:
de una circunferencia es:
donde  es la longitud del radio.
es la longitud del radio.
Pues  (número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:
(número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:
-
-
Ecuaciones de la circunferencia
Ecuación en coordenadas cartesianas
En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (h, k) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación
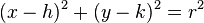 .
.
Cuando el centro está en el origen (0, 0), la ecuación anterior se simplifica al
-
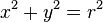 .
.
La circunferencia con centro en el origen y de radio la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria.
De la ecuación general de una circunferencia,
se deduce:
resultando:
Si conocemos los puntos extremos de un diámetro:  ,
,
la ecuación de la circunferencia es:
Ecuación vectorial de la circunferencia
La circunferencia con centro en el origen y radio R, tiene por ecuación vectorial:  .Donde
.Donde  es el parámetro de la curva, además cabe destacar que
es el parámetro de la curva, además cabe destacar que ![\theta\in[0,2\pi]](http://upload.wikimedia.org/math/b/1/1/b1194bd0172849450c424366d14501a0.png) . Se puede deducir fácilmente desde la ecuación cartesiana, ya que el componente X y el componente Y, al cuadrado y sumados deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
. Se puede deducir fácilmente desde la ecuación cartesiana, ya que el componente X y el componente Y, al cuadrado y sumados deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
Ecuación en coordenadas polares
Cuando la circunferencia tiene centro en el origen y el radio es c, se describe en coordenadas polares como 
Cuando el centro no está en el origen, sino en el punto 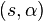 y el radio es
y el radio es  , la ecuación se transforma en:
, la ecuación se transforma en:
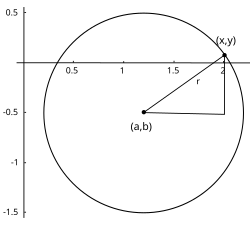
Ecuación en coordenadas paramétricas
La circunferencia con centro en (a, b) y radio c se parametriza con funciones trigonométricas como:
y con funciones racionales como
Área del círculo delimitado por una circunferencia
El área del círculo delimitado por la circunferencia es:
Esta última fórmula se deduce sabiendo que el área de cualquier polígono regular es igual al producto del apotema por el perímetro del polígono dividido entre 2, es decir: 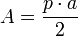 .
.
Considerando la circunferencia como el caso límite de un polígono regular de infinitos lados, entonces, el apotema coincide con el radio, y el perímetro con la longitud de la circunferencia, por tanto:
Otras propiedades
El segundo teorema de Tales muestra que si los tres vértices de un triángulo están sobre una circunferencia dada, siendo uno de sus lados el diámetro de la circunferencia, entonces, el ángulo opuesto a éste lado es un ángulo recto (véase arco capaz).
Dados tres puntos cualesquiera no alineados, existe una única circunferencia que contiene a estos tres puntos (esta circunferencia estará circunscrita al triángulo definido por estos puntos). Dados tres puntos no alineados en el plano cartesiano 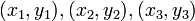 , la ecuación de la circunferencia está dada de forma simple por la determinante matricial:
, la ecuación de la circunferencia está dada de forma simple por la determinante matricial:
Circunferencia en topología
En topología, se denomina circunferencia a cualquier curva cerrada que sea homeomorfa a la circunferencia usual de la geometría (es decir, la esfera 1–dimensional). Se la puede definir como el espacio cociente determinado al identificar los dos extremos de un segmento cerrado.
Los geómetras llaman 3-esfera a la superficie de la esfera, mientras que topólogos se refieren a ella como 2-esfera y la indican como .
.
Sistema de Ecuaciones de 3x3. Método matricial
Mientras las ecuaciones lineales de dos dimensiones representan rectas, las ecuaciones lineales con tres variables: ax + by +cz = d ,representan planos.
Para representar un plano se necesitan tres puntos que no estén en la misma recta. Y estos se determinan encontrando tres soluciones de la ecuación a representar.
![]() Ejemplo:
Ejemplo:
Representar gráficamente la ecuación 4x + 3y + 2z = 12
Solución:
Buscamos tres triplas que satisfagan la ecuación.
Las triplas mas fáciles de encontrar son las correspondientes a los puntos de intersección del plano con cada uno de los ejes. Estas se obtienen al hacer que dos de las tres variables sean cero y resolviendo la ecuación para la otra.


En matemáticas se define el determinante como una forma multilineal alternada de un cuerpo En. Esta definición indica una serie de propiedades matemáticas y generaliza el concepto de determinante haciéndolo aplicable en numerosos campos. Sin embargo, el concepto de determinante o de volumen orientado fue introducido para estudiar el número de soluciones de los sistemas lineales de ecuaciones.
Historia de los determinantes [editar]
Los determinantes fueron introducidos en Occidente a partir del siglo XVI, esto es, antes que las matrices, que no aparecieron hasta el siglo XIX. Conviene recordar que los chinos (Hui, Liu. iuzhang Suanshu o Los nueve capítulos del arte matemático.) fueron los primeros en utilizar la tabla de ceros y en aplicar un algoritmo que, desde el Siglo XIX, se conoce con el nombre de Eliminación de Gauss-Jordan.
Primeros cálculos de determinantes [editar]
En su sentido original, el determinante determina la unicidad de la solución de un sistema de ecuaciones lineales. Fue introducido para el caso de orden 2 por Cardano en 1545 en su obra Ars Magna presentado como una regla para la resolución de sistemas de dos ecuaciones con dos incógnitas. Esta primera fórmula lleva el nombre de regula de modo.
El japonés Kowa Seki introdujo los determinantes de orden 3 y 4 en la misma época que el alemán Leibniz.
La aparición de determinantes de órdenes superiores tardó aún más de cien años en llegar. Curiosamente el japonés Kowa Seki y el alemán Leibniz otorgaron los primeros ejemplos casi simultáneamente.
Leibniz estudió los distintos tipos de sistemas de ecuaciones lineales. Al no disponer de la notación matricial, representaba los coeficientes de las incógnitas con una pareja de índices: así pues escribía ij para representar ai, j. En 1678 se interesó por un sistema de tres ecuaciones con tres incógnitas y obtuvo, para dicho ejemplo, la fórmula de desarrollo a lo largo de una columna. El mismo año, escribió un determinante de orden 4, correcto en todo salvo en el signo.[1] Leibniz no publicó este trabajo, que pareció quedar olvidado hasta que los resultados fueron redescubiertos de forma independiente cincuenta años más tarde.
En el mismo periodo, Kowa Seki publicó un manuscrito sobre los determinantes, donde se hallan fórmulas generales difíciles de interpretar. Parece que se dan fórmulas correctas para determinantes de tamaño 3 y 4, y de nuevo los signos mal para los determinantes de tamaño superior.[2] El descubrimiento se queda sin futuro a causa del cierre de Japón al mundo exterior por órdenes del shōgun, lo que se ve reflejado en la expulsión de los Jesuitas en 1638.
Determinantes de cualquier dimensión
En 1748, en un tratado póstumo de álgebra de MacLaurin aparece la regla para obtener la solución de un sistema de n ecuaciones lineales con n incógnitas cuando n es 2, 3 o 4 mediante el uso de determinantes.[3] [4] En 1750, Cramer da la regla para el caso general, aunque no ofrece demostración alguna. Los métodos de cálculo de los determinantes son hasta entonces delicados debido a que se basan en la noción de signatura de una permutación.[5]
Los matemáticos se familiarizan con este nuevo objeto a través de los artículos de Bézout en 1764, de Vandermonde en 1771 (que proporciona concretamente el calculo del determinante de la actual Matriz de Vandermonde). En 1772, Laplace establece las reglas de recurrencia que llevan su nombre. En el año siguiente, Lagrange descubre la relación entre el cálculo de los determinantes y el de los volúmenes.[4]
Gauss utiliza por primera vez el término « déterminante », en las Disquisitiones arithmeticae en 1801. Lo empleaba para lo que hoy día denominamos discriminante de una cuádrica y que es un caso particular de determinante moderno. Igualmente estuvo cerca de obtener el teorema del determinante de un producto.
Aparición de la noción moderna de determinante
Cauchy fue el primero en emplear el término determinante con su significado moderno. Se encargó de realizar una síntesis de los conocimientos anteriores y publicó en 1812 la fórmula y demostración del determinante de un producto junto con el enunciado y demostración de la regla de Laplace[6] . Ese mismo año Binet ofreció otra demostración (incorrecta) para la fórmula del determinante de un producto.[6] [4] Paralelamente Cauchy establece las bases del estudio de la reducción de endomorfismos.
En 1825 Heinrich F. Scherk publicó nuevas propiedades de los determinantes.[6] . Entre las propiedades halladas estaba la propiedad de que en una matriz en la que una fila es combinación lineal de varias de las demás filas de la matriz el determinante es cero.
Con la publicación de sus tres tratados sobre determinantes en 1841 en la revista Crelle, Jacobi aporta a la noción una gran notoriedad. Por primera vez presenta métodos sistemáticos de cálculo bajo una forma algorítmica. Del mismo modo, hace posible la evaluación del determinante de funciones con instauración del jacobiano, lo que supone un gran avance en la abstracción del concepto del determinante.
El cuadro matricial es introducido por los trabajos de Cayley y James Joseph Sylvester[cita requerida]. Cayley es también el inventor de la notación de los determinantes mediante barras verticales (1841[6] ) y establece la fórmula para el cálculo de la inversa de una matriz mediante determinantes(1858[4] ).
La teoría se ve reforzada por el estudio de determinantes que tienen propiedades de simetría particulares y por la introducción del determinante en nuevos campos de las matemáticas, como el wronskiano en el caso de las ecuaciones diferenciales lineales.
Métodos de cálculo
Para el cálculo de determinantes de matrices de cualquier orden, existe una regla recursiva (teorema de Laplace) que reduce el cálculo a sumas y restas de varios determinantes de un orden inferior. Este proceso se puede repetir tantas veces como sea necesario hasta reducir el problema al cálculo de múltiples determinantes de orden tan pequeño como se quiera. Sabiendo que el determinante de un escalar es el propio escalar, es posible calcular el determinante de cualquier matriz aplicando dicho teorema.
ación lineal.





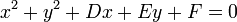

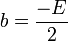





![x=a + c \cos t,\ y=b+c\sin t,\qquad t\in[0,2\pi]](http://upload.wikimedia.org/math/f/d/0/fd08b31a7dac369664c95f143fb10657.png)