blogs de matematicas: mayo 2010

domingo, 23 de mayo de 2010

sábado, 22 de mayo de 2010

PARABOLA

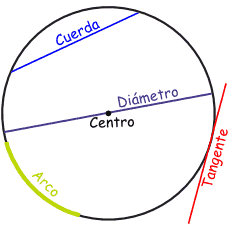
En matemática, la parábola (del griego παραβολή) es la sección cónica resultante de cortar un cono recto con un plano paralelo a su generatriz.^[1]

Se define también como el lugar geométrico de los puntos que equidistan de una recta (eje o directriz) y un punto fijo llamado foco.

En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividad semejante o semejanza.

La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas son parábolas. Por ejemplo, la trayectoria ideal del movimiento de los cuerpos bajo la influencia de la gravedad.

Secciones cónicas.

La trayectoria de una pelota que rebota recorre parábolas.

Historia

La tradición reza que las secciones cónicas fueron descubiertas por Menecmo en su estudio del problema de la duplicación del cubo,^[2] donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Eratóstenes.^[3]

Sin embargo, el primero en usar el término parábola fue Apolonio de Perge en su tratado Cónicas,^[4] considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.

Si un cono es cortado por un plano a través de su eje, y también es cortado por otro plano que corte la base del cono en una línea recta perpendicular a la base del triángulo axial, y si adicionalmente el diámetro de la sección es paralelo a un lado del triángulo axial, entonces cualquier línea recta que se dibuje desde la sección de un cono a su diámetro paralelo a la sección común del plano cortante y una de las bases del cono, será igual en cuadrado al rectángulo contenido por la línea recta cortada por ella en el diámetro que inicia del vértice de la sección y por otra línea recta que está en razón a la línea recta entre el ángulo del cono y el vértice de la sección que el cuadrado en la base del triángulo axial tiene al rectángulo contenido por los dos lados restantes del triángulo. Y tal sección será llamada una parábola

Apolonio de Perge

Es Apolonio quien menciona que un espejo parabólico refleja de forma paralela los rayos emitidos desde su foco, propiedad usada hoy en día en las antenas satelitales. La parábola también fue estudiada por Arquímedes, nuevamente en la búsqueda de una solución para un problema famoso: la cuadratura del círculo, dando como resultado el libro Sobre la cuadratura de la parábola.

Propiedades geométricas

Diferentes elementos de una parábola.

Aunque la definición original de la parábola es la relativa a la sección de un cono recto por un plano paralelo a su directriz, actualmente es más común definir la parábola como un lugar geométrico:

Una parábola es el lugar geométrico de los puntos equidistantes de una recta dada, llamada directriz, y un punto fijo que se denomina foco.

De esta forma, una vez fija una recta y un punto se puede construir una parábola que los tenga por foco y directriz de acuerdo a la siguiente construcción. Sea T un punto cualquiera de la recta directriz. Se une con el foco dado F y a continuación se traza la mediatriz (o perpendicular por el punto medio) del segmento TF. La intersección de la mediatriz con la perpendicular por T a la directriz da como resultado un punto P que pertenece a la parábola. Repitiendo el proceso para diferentes puntos T se puede aproximar tantos puntos de la parábola como sea necesario.

De la construcción anterior se puede probar que la parábola es simétrica respecto a la línea perpendicular a la directriz y que pasa por el foco. Al punto de intersección de la parábola con tal línea (conocida como eje de la parábola) se le conoce como vértice de la parábola y es el punto cuya distancia a la directriz es mínima. La distancia entre el vértice y el foco se conoce como Distancia focal o Radio focal.

Los puntos de la parábola están a la misma distancia del foco F y de la recta directriz.

Construcción de puntos
en una parábola.

Lado recto

El lado recto mide 4 veces la distancia focal

Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto.

La longitud del lado recto es siempre 4 veces la distancia focal.

Siendo D, E los extremos del lado recto y T, U las respectivas proyecciones sobre la directriz, denotando por W la proyección del foco F sobre la directriz, se observa que FEUW y DFWT son cuadrados, y sus lados miden FW=2FV. Por tanto el segmento DE es igual a 4 veces el segmento FV (la distancia focal).

Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de 45° con el mismo, consecuencia de que FEUW y DFWT sean cuadrados, junto con la construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la directriz, precisamente en el punto de proyección W del foco, propiedades que pueden ser aprovechadas para construir una aproximación geométrica del foco y la directriz cuando éstos son desconocidos.

Semejanza de todas las parábolas

Todas las parábolas son similares, es únicamente la escala la que crea la apariencia de que tienen formas diferentes.

Dado que la parábola es una sección cónica, también puede describirse como la única sección cónica que tiene excentricidad e = 1. La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.

Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las parábolas tienen la misma forma, pero la escala (zoom) crea la ilusión de que hay parábolas de formas diferentes.

Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma curva, salvo su escala, que depende de la distancia del punto a la directriz.

Tangentes a la parábola

La tangente bisecta el ángulo entre el foco, el punto de tangencia y su proyección.

Un resultado importante en relación a las tangentes de una parábola establece:

La tangente biseca el ángulo entre el foco, el punto de tangencia y su proyección.

En lo sucesivo, F denotará el foco de una parábola, P un punto de la misma y T su proyección sobre la directriz. Retomando la construcción dada para encontrar puntos de una parábola, sea MP la mediatriz del triángulo FPT, el cual es isósceles y por tanto biseca al ángulo FPT. Lo único que hay que verificar ahora es que MP también es la tangente en el punto P. Sea Q otro punto de la parábola y sea U su proyección en la directriz.

Puesto que FQ=QU y QU, entonces FQ. Dado que esto es cierto para cualquier otro punto de la parábola, se concluye que toda la parábola está de un mismo lado de MP, y como la desigualdad es estricta, no hay otro punto de la parábola que toque a la recta MP, esto quiere decir que MP es la tangente de la parábola en P.

Aplicaciones prácticas

Una consecuencia de gran importancia es que la tangente refleja los rayos paralelos al eje de la parábola en dirección al foco. Las aplicaciones prácticas son muchas: las antenas satelitales y radiotelescopios aprovechan el principio concentrando señales recibidas desde un emisor lejano en un receptor colocado en la posición del foco.

La concentración de la radiación solar en un punto, mediante un reflector parabólico tiene su aplicación en pequeñas cocinas solares y grandes centrales captadoras de energía solar.

Análogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes para poder enviar haces de luz paralelos emanados de una fuente en posición focal. Los rayos convergen o divergen si el emisor se deplaza de la posición focal.

La parábola refleja sobre el foco los rayos paralelos al eje. Analogamente, un emisor situado en el foco, enviará un haz de rayos paralelos al eje.

Los radiotelescopios concentran los haces de señales en un receptor situado en el foco. El mismo principio se aplica en una antena de radar.

Cocina solar de concentrador parabólico. El mismo método se emplea en las grandes centrales captadoras de energía solar.

Los faros de los automóviles envían haces de luz paralelos, si la bombilla se situa en el foco de una superficie parabólica.

Ecuaciones de la parábola

Parábolas tipo y=ax², con a=4, 1, 1/4 y 1/10.

Prueba geométrica de la relación y=ax².

Con el advenimiento de la geometría analítica se inició un estudio de las formas geométricas basado en ecuaciones y coordenadas.

Una parábola cuyo vértice está en el origen y su eje coincide con el eje de las ordenadas, tiene una ecuación de la forma y=ax² donde el parámetro a especifica la escala de la parábola, incorrectamente descrita como la forma de la parábola, ya que como se dijo antes, todas las parábolas tienen la misma forma. Cuando el parámetro es positivo, la parábola se abre «hacia arriba» y cuando es negativo se abre «hacia abajo».

Si bien, la expresión en forma de ecuación no fue posible hasta el desarrollo de la geometría analítica, la relación geométrica expresada en la ecuación anterior ya estaba presente en los trabajos de Apolonio,^[2] y se bosquejará a continuación usando notación moderna.

Tomando nuevamente la definición de parábola como sección de un cono recto de forma paralela a la directriz, sea V un punto en el eje y sea QV perpendicular al eje. (QV corresponde al valor x en la versión analítica y PV al valor y). Considerando la sección circular que pasa por Q y es paralela a la base del cono, obtenemos H, K paralelos a B y C.

Por el teorema de potencia de un punto:

$QV^2 = HV\cdot VK$ .

Al ser PM paralela a AC, los triángulos HVP, HKA y BCA son semejantes y así:

$\frac{HV}{PV} = \frac{HK}{KA} = \frac{BC}{AC}$ .

Usando nuevamente los paralelismos:

$\frac{VK}{PA} = \frac{HK}{HA} = \frac{BC}{BA}$ .

Despejando HV y VK para sustituir en la fórmula de QV² resulta en

$QV^2=HV\cdot VK=\left(\frac{BC\cdot PV}{AC}\right)\left(\frac{BC\cdot PA}{BA}\right) = \left(\frac{BC^2\cdot PA}{BA\cdot AC}\right)PV$ .

Pero el valor de $\left(\frac{BC^2\cdot PA}{BA\cdot AC}\right)$ es una constante pues no depende de la posición de V, por lo que haciendo

$a = \frac{BA\cdot AC}{BC^2\cdot PA},$

arroja la expresión moderna y=ax².

Parábolas verticales, con ecuaciones de la forma y=ax²+bx+c.

Aplicando una sustitución de coordenadas podemos obtener ahora la ecuación de una parábola vertical para cualquier posición de su vértice.

La ecuación de una parábola cuyo eje es vertical y su vértice es (u,v) tiene la forma (y-v)=a(x-u)²,

agrupando los términos y reordenando se obtiene una forma equivalente:

La ecuación de una parábola cuyo eje es vertical es de la forma $y = a x^2 + bx + c \,$ .

Si la parábola es horizontal, se obtienen ecuaciones similares pero intercambiando y por x y viceversa. Así tendríamos:

La ecuación de una parábola cuyo eje es horizontal es de la forma $x = a y^2 + by + c \,$ .

Ecuación involucrando la distancia focal [editar]

Ecuación de una parábola vertical.

Pueden haber muchas parábolas que tengan un mismo vértice (variando el parámetro a) en la primera ecuación. Sin embargo, dados dos puntos fijos, existe sólo una parábola que los tiene por vértice y foco ya que la directriz queda automáticamente fija como la perpendicular a la línea que une el foco con el vértice y a esa misma distancia del último.

Consideremos el caso especial en que el vértice es (0,0) y el foco es (0,p). La directriz es por tanto, la recta horizontal que pasa por (0,-p). A la distancia entre el vértice y el foco se le llama distancia focal, de modo que en este caso la distancia focal es igual a p. Con esta configuración se tiene:

La ecuación de una parábola con vértice en (0,0) y foco en (0,p) es $\,x^2=4py$ .

De forma alterna:

La ecuación de una parábola con vértice en (0,0) y foco en (0,p) es $y=\frac{x^2}{4p}$ .

Es de notar que el coeficiente 4p es precisamente la longitud del lado recto de la parábola.

Ambas ecuaciones se refieren a parábolas verticales que se abren «hacia arriba». La ecuación de una parábola que se abre hacia abajo es similar excepto que varía un signo. En este caso, el foco sería (0,-p) y de esta forma:

La ecuación de una parábola con vértice en (0,0) y foco en (0,-p) es $\,x^2=-4py$ .

Cuando la parábola es horizontal «hacia la derecha», se obtiene una ecuación similar intercambiando los roles de x, y:

La ecuación de una parábola con vértice en (0,0) y foco en (p,0) es $\,y^2=4px$ ,

obteniendo mediante un cambio de signo la ecuación de las parábolas hacia la izquierda.

Finalmente, las ecuaciones cuando el vértice no está en el centro se obtienen mediante una traslación. En el caso común de la parábola vertical hacia arriba se tiene

La ecuación de una parábola con vértice en (h, k) y foco en (h, k+p) es $\,(x-h)^2=4p(y-k)$ ,

mientras que para la parábola horizontal se intercambia x con y:.

La ecuación de una parábola con vértice en (h, k) y foco en (h+p, k) es $\,(y-k)^2=4p(x-h)$ .

Ecuación general de una parábola [editar]

Hasta ahora se han descrito parábolas con sus ejes paralelos a alguno de los ejes de coordenadas. De esta forma las fórmulas son funciones de x ó de y. Pero una parábola puede tener su eje inclinado con respecto a un par de ejes de coordenadas ortogonales.

La expresión algebraica que describe una parábola que ocupe cualquier posición en un plano es:

$\,a x^2 + b xy + c y^2 + d x + e y + f = 0$

si y sólo si

$\, b^2 - 4ac = 0$

y los coeficientes a y c no pueden ser simultáneamente nulos

Mediante traslaciones y rotaciones es posible hallar un sistema de referencia en el que la ecuación anterior se exprese mediante una fórmula algebraica de la forma

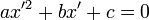$\,a x'^2 + b x' + c = 0$ , donde a es distinto de cero.

viernes, 21 de mayo de 2010

COMPLEMENTOS DE LA CONSULTA

Linea secante

Linea tangente

DOMINIO ( Complemento de la consulta)

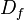En matemáticas, el dominio (conjunto de definición o conjunto de partida) de una función $f \colon X \to Y \,$ es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota $Dom_f\,$ o bien $D_f\,$ y está definido por:

$D_f = \; \left\{x \in X | \exists y \in Y: f(x)=y\right\}$
Propiedades

Dadas dos funciones reales:

$f \colon X_1 \to \R\, \qquad \mbox{y}\quad g \colon X_2 \to \R\,$

Se tienen las siguientes propiedades:

$D_{(f+g)} = X_1\cap X_2$
$D_{(f-g)} = X_1\cap X_2$
$D_{(f\cdot g)}\ = X_1\cap X_2$
$D_{(f/g)} = \{x\in (X_1 \cap X_2)| g(x) \neq 0\}$

Ejemplos [editar]

Algunos dominios de funciones reales de variable real:

$f(x)=x^2 \,\!$ El dominio de esta función es $\mathbb{R}$

$f(x)= \frac{1}{x}$ El dominio de esta función es $\mathbb{R}-\lbrace0\rbrace$ puesto que la función no está definida para x = 0.

$f(x)= \log(x) \,\!$ El dominio de esta función es $(0,{+}\infty)$ ya que los logaritmos están definidos sólo para números positivos.

$f(x)= \sqrt{x}$ El dominio de esta función es $\lbrack0,{+}\infty)$ porque la raíz de un número negativo no existe en el campo de los Reales.

Cálculo del dominio de una función [editar]

Para el cálculo certero del dominio de una función, debemos introducir el concepto de restricción en el campo real. Estas restricciones nos ayudarán a identificar la existencia del dominio de una función. Las más usadas son:

Raíz enésima de f(x) [editar]

No existe restricción si n es impar, pero si "n" es par, la función f(x) necesariamente deberá ser mayor no estricto de cero, ya que las raíces negativas no están definidas en el campo real. Por ejemplo:

$y= \sqrt{7x-21}$

El índice de la raíz es par (2), por tanto

$7 x - 21 > = 0$ despejando tenemos que

x>=3 El dominio entonces será el conjunto de todos los reales en el intervalo [3,+∞)

Logaritmo de f(x)

La restricción está al estudiar las propiedades de los logaritmos las cuales nos dicen que estos no están definidos para números negativos, por tanto toda función contenida dentro de un logaritmo es necesariamente mayor estricto de cero. Por ejemplo:

$l o g (x 2 - 9)$ Por la propiedad anteriormente citada tenemos que para que esta función exista, necesariamente

$x 2 - 9 > 0$ despejando obtendremos dos soluciones $x > 3$ y $x < - 3$ . La unión de ambas soluciones representa el dominio de la función, que está definida como el conjunto (-∞, -3) U (3, +∞).

Fracciones

Otras propiedades de las matemáticas nos pueden ayudar a obtener el dominio de una función y excluir puntos donde esta no está definida, por ejemplo, una función que tenga forma de fracción no estará definida cuando el denominador valga cero, ya que esto es una indeterminación que daría una tendencia al infinito. Veamos

la función $y= \frac {7-3x}{10x-2}$ no estará definida cuando $10 x - 2 = 0$ , despejando $x = 1 / 5$ , es decir la variable x debe tener un valor diferente para poder existir, ya que en ese punto no está definida, por tanto el dominio de esta función será el conjunto de todos los reales menos ese punto. Su notación será R-{1/5}, que se lee, el conjunto de todos los reales menos el punto 0,20.

El grado de dificultad se incrementa cuando buscamos el dominio de una función con variable en el denominador contenida dentro de un radical de índice par o logaritmo, ya que esto nos traslada a resolver una desigualdad. No obstante, el método de polos y ceros nos permite resolver esta clase de inecuaciones con facilidad.

Ejemplo [editar]

Para evidenciar este caso veamos este problema. Hallar el dominio de la siguiente función:

$f(x) = log( \frac {5x+1}{3x-2} \ ),\!$

Para que esta función exista, necesariamente

$\text{[math]}$ 0,\!" src="http://upload.wikimedia.org/math/4/c/e/4ce3a3b33ce7b052dbd2c0bffcd0d5c9.png">

Ya que no existe logaritmo de expresiones negativas. La solución de esta desigualdad, es explicada paso por paso en el artículo polos y ceros anteriormente citado, su solución constituirá el dominio de la función que en este caso será:

solución: (-∞, -1/5) U (2/3, +∞)

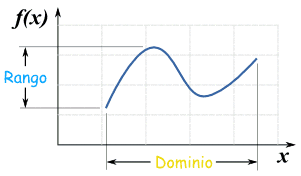IMAGEN PARA DOMINIO Y RANGO

FUNCION UNO A UNO

Función uno uno

Ya sabes que la definición de una función exige que a cada elemento del dominio le corresponda un solo elemento del recorrido. En caso de que también a cada elemento del recorrido le corresponda un solo elemento del dominio, se tiene una función uno a uno.

Ilustración de funcion 1 - 1

Aquí los pares ordenados son: ( -1, -26 ), ( 10, a ) , ( 0, 0 ); para cada valor del recorrido existe un solo valor en el dominio.

Una función f se dice que es uno uno si para cada pareja de elementos diferentes en el dominio de f, x₁ x_{2 ,}se tiene también elementos diferentes en el recorrido de f, f(x₁) f(x₂).

La siguiente ilustración muestra una función que no es uno – uno

Aquí los pares oredenados son: ( -1, -26 ), ( 10, -26 ), (0, 0). Observa que dos valores del dominio, -1 y 10 corresponden a un mismo valor en el recorrido, -26. Esto es, hay dos pares ordenados que tienen la misma segunda componente, pero diferentes primera componente.

Ver ilustración definición 1 de la página 183.

Cómo determinar que una función es uno – uno cuando dan la ecuación:

Escoge valores arbitrarios; al igualar valores del recorrido se debe obtener los correspondientes valores iguales para el dominio.

Si f(x₁) = f(x₂) entonces ver que x₁ = x₂

Ejemplo1

Ver si F(x) = 2x es una función 1-1.

Considera dos variables dependientes arbitrarios.

F(x₁) = F(x₂) IGUALES valores del recorrido

2x₁= 2 x₂ (sustituye la regla)

x₁ = x₂ (al dividir por 2 ambos lados ) IGUALES valores del dominio

F(x) = 2x es una función 1-1.

_{Para demostrar que una función no es uno-uno basta con ilustrar con un ejemplo para un caso particular.}

Ejemplo 2

Función estrictamente creciente en un intervalo

Una función $\mathrm{f} \left( \, x \, \right)$ es estrictamente creciente en un intervalo

  \, a, \, b \,

\right)" alt="\left(

  \, a, \, b \,

\right)" class="tex"> , si para dos valores cualesquiera del intervalo, $x_1$ y $x_2$ , se cumple que:

 \, - \, x_1} > 0

" alt="\frac{\mathrm{f}\left( \, x_2 \, \right) \, - \, \mathrm{f}\left( \, x_1 \, \right)}{x_2

 \, - \, x_1} > 0

" class="tex">

Cuando en la gráfica de una función estrictamente creciente nos movemos hacia la derecha tambien nos movemos hacia arriba:

x_1 \Rightarrow \mathrm{f} \left( \, x_2 \, \right) > \mathrm{f} \left( \, x_1 \, \right)" alt="x_2 > x_1 \Rightarrow \mathrm{f} \left( \, x_2 \, \right) > \mathrm{f} \left( \, x_1 \, \right)" class="tex">

Una función $f$ es estrictamente creciente en el punto de abcisa $x \, = \, a$ si existe algun número positivo $h$ tal que

" alt="\mathrm{f}

" class="tex"> es estrictamente creciente en el intervalo

  \, x \, - \, h, \, x \, + \, h \,

\right)" alt="\left(

  \, x \, - \, h, \, x \, + \, h \,

\right)" class="tex">.

De esta esta definición se deduce que si $\mathrm{f}$ es derivable en $x \, = \, a$ y $f$ es estrictamente creciente en el punto de abcisa $x \, = \, a$ , entonces $\mathrm{f}^\prime \left( \, a \, \right) \ge 0$ .

Función creciente en un intervalo

Una función $\mathrm{f} \left( \, x \, \right)$ es creciente en un intervalo

  \, a, \, b \,

\right)" alt="\left(

  \, a, \, b \,

\right)" class="tex"> , si para dos valores cualesquiera del intervalo, $x_1$ y $x_2$ , se cumple que:

 \, - \, x_1} \ge 0

" alt="\frac{\mathrm{f}\left( \, x_2 \, \right) \, - \, \mathrm{f}\left( \, x_1 \, \right)}{x_2

 \, - \, x_1} \ge 0

" class="tex">

Función estrictamente decreciente en un intervalo

Una función $\mathrm{f} \left( \, x \, \right)$ es estrictamente decreciente en un intervalo

  \, a, \, b \,

\right)" alt="\left(

  \, a, \, b \,

\right)" class="tex"> , si para dos valores cualesquiera del intervalo, $x_1$ y $x_2$ , se cumple que:

 \, - \, x_1} <> " alt="\frac{\mathrm{f}\left( \, x_2  \, \right) \, - \, \mathrm{f}\left( \, x_1 \, \right)}{x_2 
  \, - \, x_1} <> " class="tex">

Cuando en la gráfica de una función estrictamente decreciente nos movemos hacia la derecha tambien nos movemos hacia abajo:

x_1 \Rightarrow \mathrm{f} \left( \, x_2 \, \right) < \mathrm{f} \left( \, x_1 \, \right)" alt="x_2 > x_1 \Rightarrow \mathrm{f} \left( \, x_2 \, \right) < \mathrm{f} \left( \, x_1 \, \right)" class="tex">

Una función $f$ es estrictamente decreciente en el punto de abcisa $x \, = \, a$ si existe algun número positivo $h$ tal que

" alt="\mathrm{f}

" class="tex"> es estrictamente decreciente en el intervalo

  \, x \, - \, h, \, x \, + \, h \,

\right)" alt="\left(

  \, x \, - \, h, \, x \, + \, h \,

\right)" class="tex">.

De esta esta definición se deduce que si $\mathrm{f}$ es derivable en $x \, = \, a$ y $f$ es estrictamente decreciente en el punto de abcisa $x \, = \, a$ , entonces $\mathrm{f}^\prime \left( \, a \, \right) \le 0$ .

Función decreciente en un intervalo

Una función $\mathrm{f} \left( \, x \, \right)$ es decreciente en un intervalo

  \, a, \, b \,

  \, a, \, b \,

\right)" class="tex"> , si para dos valores cualesquiera del intervalo, $x_1$ y $x_2$ , se cumple que:

blogs de matematicas

domingo, 23 de mayo de 2010

sábado, 22 de mayo de 2010

Historia

Propiedades geométricas

Lado recto

Semejanza de todas las parábolas

Tangentes a la parábola

Aplicaciones prácticas

Ecuaciones de la parábola

Ecuación involucrando la distancia focal [editar]

Ecuación general de una parábola [editar]

viernes, 21 de mayo de 2010

Propiedades

Ejemplos [editar]

Cálculo del dominio de una función [editar]

Raíz enésima de f(x) [editar]

Logaritmo de f(x)

Fracciones

Ejemplo [editar]

Función uno uno

Función estrictamente creciente en un intervalo

Función creciente en un intervalo

Función estrictamente decreciente en un intervalo

Función decreciente en un intervalo

Seguidores

Archivo del blog