blogs de matematicas

COMPLEMENTOS DE LA CONSULTA

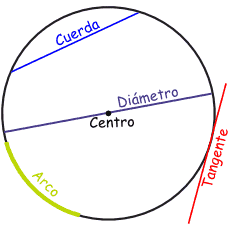
Linea secante

Linea tangente

DOMINIO ( Complemento de la consulta)

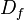En matemáticas, el dominio (conjunto de definición o conjunto de partida) de una función $f \colon X \to Y \,$ es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota $Dom_f\,$ o bien $D_f\,$ y está definido por:

$D_f = \; \left\{x \in X | \exists y \in Y: f(x)=y\right\}$
Propiedades

Dadas dos funciones reales:

$f \colon X_1 \to \R\, \qquad \mbox{y}\quad g \colon X_2 \to \R\,$

Se tienen las siguientes propiedades:

$D_{(f+g)} = X_1\cap X_2$
$D_{(f-g)} = X_1\cap X_2$
$D_{(f\cdot g)}\ = X_1\cap X_2$
$D_{(f/g)} = \{x\in (X_1 \cap X_2)| g(x) \neq 0\}$

Ejemplos [editar]

Algunos dominios de funciones reales de variable real:

$f(x)=x^2 \,\!$ El dominio de esta función es $\mathbb{R}$

$f(x)= \frac{1}{x}$ El dominio de esta función es $\mathbb{R}-\lbrace0\rbrace$ puesto que la función no está definida para x = 0.

$f(x)= \log(x) \,\!$ El dominio de esta función es $(0,{+}\infty)$ ya que los logaritmos están definidos sólo para números positivos.

$f(x)= \sqrt{x}$ El dominio de esta función es $\lbrack0,{+}\infty)$ porque la raíz de un número negativo no existe en el campo de los Reales.

Cálculo del dominio de una función [editar]

Para el cálculo certero del dominio de una función, debemos introducir el concepto de restricción en el campo real. Estas restricciones nos ayudarán a identificar la existencia del dominio de una función. Las más usadas son:

Raíz enésima de f(x) [editar]

No existe restricción si n es impar, pero si "n" es par, la función f(x) necesariamente deberá ser mayor no estricto de cero, ya que las raíces negativas no están definidas en el campo real. Por ejemplo:

$y= \sqrt{7x-21}$

El índice de la raíz es par (2), por tanto

$7 x - 21 > = 0$ despejando tenemos que

x>=3 El dominio entonces será el conjunto de todos los reales en el intervalo [3,+∞)

Logaritmo de f(x)

La restricción está al estudiar las propiedades de los logaritmos las cuales nos dicen que estos no están definidos para números negativos, por tanto toda función contenida dentro de un logaritmo es necesariamente mayor estricto de cero. Por ejemplo:

$l o g (x 2 - 9)$ Por la propiedad anteriormente citada tenemos que para que esta función exista, necesariamente

$x 2 - 9 > 0$ despejando obtendremos dos soluciones $x > 3$ y $x < - 3$ . La unión de ambas soluciones representa el dominio de la función, que está definida como el conjunto (-∞, -3) U (3, +∞).

Fracciones

Otras propiedades de las matemáticas nos pueden ayudar a obtener el dominio de una función y excluir puntos donde esta no está definida, por ejemplo, una función que tenga forma de fracción no estará definida cuando el denominador valga cero, ya que esto es una indeterminación que daría una tendencia al infinito. Veamos

la función $y= \frac {7-3x}{10x-2}$ no estará definida cuando $10 x - 2 = 0$ , despejando $x = 1 / 5$ , es decir la variable x debe tener un valor diferente para poder existir, ya que en ese punto no está definida, por tanto el dominio de esta función será el conjunto de todos los reales menos ese punto. Su notación será R-{1/5}, que se lee, el conjunto de todos los reales menos el punto 0,20.

El grado de dificultad se incrementa cuando buscamos el dominio de una función con variable en el denominador contenida dentro de un radical de índice par o logaritmo, ya que esto nos traslada a resolver una desigualdad. No obstante, el método de polos y ceros nos permite resolver esta clase de inecuaciones con facilidad.

Ejemplo [editar]

Para evidenciar este caso veamos este problema. Hallar el dominio de la siguiente función:

$f(x) = log( \frac {5x+1}{3x-2} \ ),\!$

Para que esta función exista, necesariamente

$\text{[math]}$ 0,\!" src="http://upload.wikimedia.org/math/4/c/e/4ce3a3b33ce7b052dbd2c0bffcd0d5c9.png">

Ya que no existe logaritmo de expresiones negativas. La solución de esta desigualdad, es explicada paso por paso en el artículo polos y ceros anteriormente citado, su solución constituirá el dominio de la función que en este caso será:

solución: (-∞, -1/5) U (2/3, +∞)

IMAGEN PARA DOMINIO Y RANGO

FUNCION UNO A UNO

Función uno uno

Ya sabes que la definición de una función exige que a cada elemento del dominio le corresponda un solo elemento del recorrido. En caso de que también a cada elemento del recorrido le corresponda un solo elemento del dominio, se tiene una función uno a uno.

Ilustración de funcion 1 - 1

Aquí los pares ordenados son: ( -1, -26 ), ( 10, a ) , ( 0, 0 ); para cada valor del recorrido existe un solo valor en el dominio.

Una función f se dice que es uno uno si para cada pareja de elementos diferentes en el dominio de f, x₁ x_{2 ,}se tiene también elementos diferentes en el recorrido de f, f(x₁) f(x₂).

La siguiente ilustración muestra una función que no es uno – uno

Aquí los pares oredenados son: ( -1, -26 ), ( 10, -26 ), (0, 0). Observa que dos valores del dominio, -1 y 10 corresponden a un mismo valor en el recorrido, -26. Esto es, hay dos pares ordenados que tienen la misma segunda componente, pero diferentes primera componente.

Ver ilustración definición 1 de la página 183.

Cómo determinar que una función es uno – uno cuando dan la ecuación:

Escoge valores arbitrarios; al igualar valores del recorrido se debe obtener los correspondientes valores iguales para el dominio.

Si f(x₁) = f(x₂) entonces ver que x₁ = x₂

Ejemplo1

Ver si F(x) = 2x es una función 1-1.

Considera dos variables dependientes arbitrarios.

F(x₁) = F(x₂) IGUALES valores del recorrido

2x₁= 2 x₂ (sustituye la regla)

x₁ = x₂ (al dividir por 2 ambos lados ) IGUALES valores del dominio

F(x) = 2x es una función 1-1.

_{Para demostrar que una función no es uno-uno basta con ilustrar con un ejemplo para un caso particular.}

Ejemplo 2

Función estrictamente creciente en un intervalo

Una función $\mathrm{f} \left( \, x \, \right)$ es estrictamente creciente en un intervalo

  \, a, \, b \,

\right)" alt="\left(

  \, a, \, b \,

\right)" class="tex"> , si para dos valores cualesquiera del intervalo, $x_1$ y $x_2$ , se cumple que:

 \, - \, x_1} > 0

" alt="\frac{\mathrm{f}\left( \, x_2 \, \right) \, - \, \mathrm{f}\left( \, x_1 \, \right)}{x_2

 \, - \, x_1} > 0

" class="tex">

Cuando en la gráfica de una función estrictamente creciente nos movemos hacia la derecha tambien nos movemos hacia arriba:

x_1 \Rightarrow \mathrm{f} \left( \, x_2 \, \right) > \mathrm{f} \left( \, x_1 \, \right)" alt="x_2 > x_1 \Rightarrow \mathrm{f} \left( \, x_2 \, \right) > \mathrm{f} \left( \, x_1 \, \right)" class="tex">

Una función $f$ es estrictamente creciente en el punto de abcisa $x \, = \, a$ si existe algun número positivo $h$ tal que

" alt="\mathrm{f}

" class="tex"> es estrictamente creciente en el intervalo

  \, x \, - \, h, \, x \, + \, h \,

\right)" alt="\left(

  \, x \, - \, h, \, x \, + \, h \,

\right)" class="tex">.

De esta esta definición se deduce que si $\mathrm{f}$ es derivable en $x \, = \, a$ y $f$ es estrictamente creciente en el punto de abcisa $x \, = \, a$ , entonces $\mathrm{f}^\prime \left( \, a \, \right) \ge 0$ .

Función creciente en un intervalo

Una función $\mathrm{f} \left( \, x \, \right)$ es creciente en un intervalo

  \, a, \, b \,

\right)" alt="\left(

  \, a, \, b \,

\right)" class="tex"> , si para dos valores cualesquiera del intervalo, $x_1$ y $x_2$ , se cumple que:

 \, - \, x_1} \ge 0

" alt="\frac{\mathrm{f}\left( \, x_2 \, \right) \, - \, \mathrm{f}\left( \, x_1 \, \right)}{x_2

 \, - \, x_1} \ge 0

" class="tex">

Función estrictamente decreciente en un intervalo

Una función $\mathrm{f} \left( \, x \, \right)$ es estrictamente decreciente en un intervalo

  \, a, \, b \,

\right)" alt="\left(

  \, a, \, b \,

\right)" class="tex"> , si para dos valores cualesquiera del intervalo, $x_1$ y $x_2$ , se cumple que:

 \, - \, x_1} <> " alt="\frac{\mathrm{f}\left( \, x_2  \, \right) \, - \, \mathrm{f}\left( \, x_1 \, \right)}{x_2 
  \, - \, x_1} <> " class="tex">

Cuando en la gráfica de una función estrictamente decreciente nos movemos hacia la derecha tambien nos movemos hacia abajo:

x_1 \Rightarrow \mathrm{f} \left( \, x_2 \, \right) < \mathrm{f} \left( \, x_1 \, \right)" alt="x_2 > x_1 \Rightarrow \mathrm{f} \left( \, x_2 \, \right) < \mathrm{f} \left( \, x_1 \, \right)" class="tex">

Una función $f$ es estrictamente decreciente en el punto de abcisa $x \, = \, a$ si existe algun número positivo $h$ tal que

" alt="\mathrm{f}

" class="tex"> es estrictamente decreciente en el intervalo

  \, x \, - \, h, \, x \, + \, h \,

\right)" alt="\left(

  \, x \, - \, h, \, x \, + \, h \,

\right)" class="tex">.

De esta esta definición se deduce que si $\mathrm{f}$ es derivable en $x \, = \, a$ y $f$ es estrictamente decreciente en el punto de abcisa $x \, = \, a$ , entonces $\mathrm{f}^\prime \left( \, a \, \right) \le 0$ .

Función decreciente en un intervalo

Una función $\mathrm{f} \left( \, x \, \right)$ es decreciente en un intervalo

  \, a, \, b \,

  \, a, \, b \,

\right)" class="tex"> , si para dos valores cualesquiera del intervalo, $x_1$ y $x_2$ , se cumple que:

blogs de matematicas

viernes, 21 de mayo de 2010

Propiedades

Ejemplos [editar]

Cálculo del dominio de una función [editar]

Raíz enésima de f(x) [editar]

Logaritmo de f(x)

Fracciones

Ejemplo [editar]

Función uno uno

Función estrictamente creciente en un intervalo

Función creciente en un intervalo

Función estrictamente decreciente en un intervalo

Función decreciente en un intervalo

No hay comentarios:

Publicar un comentario

Seguidores

Archivo del blog