Y = mx + b
Y= -x+ 5
Por cada punto que aumente en x disminuye
 uno en y
uno en ySi la a es 0 la línea queda recta, c es el punto de corte, La ecuación pasada representa una parábola.
Si la a es negativa queda abriendo hacia abajo, si es positiva la parábola queda abriendo hacia arriba, entre mas grande el valor de a mas cerrada es la parábola.
B= es el movimiento de la parábola en el eje x, si es 0 conside con el punto de corte con el eje y, si es positiva es hacia la derecha y si es negativa hacia la izquierda. ( se inclina o se va )
C= si es 0 el punto de corte queda en el ejex, si es negativa baja al eje y y si es positiva sube.
PARTES DE LA PARABOLA
Esta consta de 3 partes
Foco, vértice directriz.
El foco es el eje de construcción de la parábola, es el centro de la directriz.
El vértice es el punto medio entre el foco la directriz.
La directriz es el eje de apoyo para la construcción de la parábola.
SIGNIFICADO DE LA ECUACION CUADRATICA
Si la parábola corta el eje y en dos partes significa que la ecuación tiene dos soluciones, cuando una ecuación no tiene solución, no toca al eje x.
Vertice es igual a con esta hallamos el punto máximo o minimo.
Ejercicio

Que es una función?
Función en matemáticas, término usado para indicar la relación o correspondencia entre dos o más cantidades. El término función fue usado por primera vez en 1637 por el matemático francés René Descartes para designar una potencia xn de la variable x. En 1694 el matemático alemán Gottfried Wilhelm Leibniz utilizó el término para referirse a varios aspectos de una curva, como su pendiente. Hasta recientemente, su uso más generalizado ha sido el definido en 1829 por el matemático alemán Peter Dirichlet. Dirichlet entendió la función como una variable y, llamada variable dependiente, cuyos valores son fijados o determinados de una forma definida según los valores que se asignen a la variable independiente x, o a varias variables independientes x1, x2, ..., xk.
Los valores, tanto de la variable dependiente, como de las variables independientes, son números reales o complejos. La expresión y = f(x), leída “y es función de x” indica la interdependencia entre las variables x e y; f(x) se daba normalmente en forma explícita, como f(x) = x2 - 3x + 5, o mediante una regla expresada en palabras, como f(x) es el primer entero mayor que x para todos aquellos x que sean reales (véase número). Si a es un número, entonces f(a) es el valor de la función para el valor x = a. Así, en el primer ejemplo, f(3) = 32 - 3 • 3 + 5 = 5, f(-4) = (-4)2 - 3(-4) + 5 = 33; en el segundo ejemplo, f(3) = f(3,1) = f() = 4.
La aparición de la teoría de conjuntos primero extendió, y luego alteró sustancialmente, el concepto de función. El concepto de función en las matemáticas de nuestros días queda ilustrado a continuación. Sean X e Y dos conjuntos con elementos cualesquiera; la variable x representa un elemento del conjunto X, y la variable y representa un elemento del conjunto Y. Los elementos de ambos conjuntos pueden ser o no números, y los elementos de X no tienen que ser necesariamente del mismo tipo que los de Y. Por ejemplo, X puede ser el conjunto de los doce signos del zodíaco e Y el conjunto de los enteros positivos. Sea P el conjunto de todos los posibles pares ordenados (x, y) y sea F un subconjunto de P con la propiedad de que si (x1, y1) y (x2, y2) son dos elementos de F, entonces si y1 ≠ y2 implica que x1 ≠ x2 esto es, F contiene no más de un par ordenado con una x dada como primer elemento. (Si x1 ≠ x2, sin embargo, puede ocurrir que y1 = y2 ). Una función queda ahora definida como el conjunto F de pares ordenados, con la condición señalada, y se escribe F: X → Y. El conjunto X1 de las x que aparecen como primer elemento de los pares ordenados de F se denomina dominio de la función F; el conjunto Y1 de las y que aparecen como segundo elemento de los pares ordenados se denomina rango de la función F. De esta manera, {(Piscis, 7), (Sagitario, 4), (Capricornio, 4)} es una función en la que X = conjunto de los doce signos del zodíaco e Y = conjunto de los enteros positivos; el dominio son los tres signos mencionados y el rango son 4 y 7.
El concepto moderno de función está relacionado con la idea de Dirichlet. Dirichlet consideró que y = x2 - 3x + 5 era una función; hoy en día, se considera que y = x2 - 3x + 5 es la relación que determina la y correspondiente a una x dada para un par ordenado de la función ; así, la relación anterior determina que (3, 5), (-4, 33) son dos de los infinitos elementos de la función. Aunque y = f(x) se usa hoy todavía, es más correcto si se lee “y está funcionalmente relacionado con x”.
Las funciones se denominan también transformaciones o aplicaciones en muchas ramas de las matemáticas. Si el conjunto Y1 es un subconjunto propio de Y (esto es, al menos una y pertenece a Y pero no a Y1), entonces F es una función, transformación o aplicación del dominio X1 en Y; si Y1 = Y, F es una función, transformación o aplicación de X1 sobre Y.
FUNCIONES ESPECIALES
Es el conjunto de funciones que intervienen en una relaciòn definida.
en ellas tenemos a la:
FUNCION LINEAL:
Una función lineal de una variable real es una función matemática de la forma:
donde m y b son constantes.
Una función lineal de una única variable independiente x suele escribirse en la forma siguiente
que se conoce como ecuación de la recta en el plano xy.
- m es denominada la pendiente de la recta.
- b es la ordenada en el origen, el valor de y en el punto x= 0.
FUNCION CONSTANTE:
Es aquella donde cada valor del codominio, no importa el valor de x, siempre será el mismo (único  valor) ya que a = 0.
valor) ya que a = 0.
Como todo número elevado a cero da uno, en este caso, la función exponencial
f(x) = m . x0 queda f(x) = m . 1 Þ f(x) = m,
donde m es un número cualquiera, por ejemplo 3.
f(x) = 3
¿ Cuál es el dominio ? Todos los reales.
¿ y la imagen ? Solamente un valor, 3.

FUNCION IDENTIDAD:
Una función identidad es una función, de un conjunto M a sí mismo, que devuelve su propio argumento.
La función identidad puede describirse de la forma siguiente:
F x)= K
- La función identidad es trivialmente idempotente, es decir:


FUNCION VALOR ABSOLUTO:
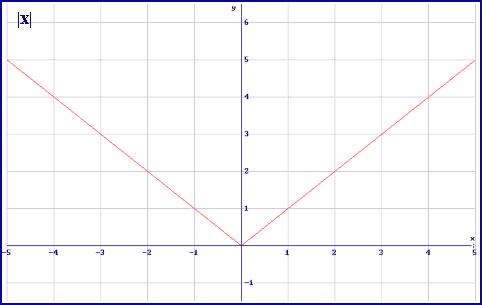
La función valor absoluto asocia a cada número su valor absoluto, es decir su valor prescindiendo del signo, esta función se puede escribir descompuesta en dos tramos:
![]()
En general cualquier función valor absoluto se puede escribir como una función a trozos. Observa la gráfica siguiente y comprueba que el valor absoluto de una función se puede obtener transformando la parte negativa en positiva.
FUNCION RAIZ CUADRATICA:
Es una función cuyo dominio es el conjunto de los reales positivos con el cero y el codominio es el conjunto de los números reales. Su fórmula es:
¦: [0; +¥ ) ® Â / ¦ (x) = Ö(x)
Clasificación:
La función raíz cuadrada es inyectiva pero no sobreyectiva porque:
1. A elementos distintos corresponden imágenes distintas;
2. El conjunto Imagen de la función es [0; +¥ ) y su Codominio es el conjunto de los números reales, por lo tanto existen elementos de él que no tienen preimágen.
Es estrictamente creciente.
La funciónraíz cuadrada no es par ni impar pues los elementos del dominio no verifican ninguna de las dos definiciones.
FUNCION MAXIMO ENTERO:
Su clasificacion es de uno en uno en Y i X que se forma por varios numeros sacados de la tabla dependiente x e y.
su simbolisaciòn es de Fx= x
FUNCION CUADRATICA:
Una función cuadrática es aquella que puede escribirse de la forma:
donde a, b y c son números reales cualesquiera y a distinto de cero. f(x) = ax2 + bx + c
Si representamos "todos" los puntos (x,f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.
Como ejemplo, ahí tienes la representación gráfica de dos funciones cuadráticas muy sencillas:



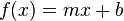





No hay comentarios:
Publicar un comentario